Als je met vaste rails werkt, zit je vast aan
vaste boogstralen.
- Boogstralen bepalen de grondplaat waar op je werkt, of andersom
de grondplaat maten bepalen welke boogstraal voor jou maximaal haalbaar is - Boogstralen bepalen hoever je kunt klimmen of dalen, omdat elke boogstraal leidt tot een bepaalde spoorlengte
- Boogstralen bepalen met hoeveel parallelle bogen je tegelijk de "hoek om" kunt gaan,
bij een bepaalde hart-op-hart afstand van die sporen - Boogstralen bepalen de maximale wagonlengtes die erop kunnen rijden, of andersom
wagonlengte kan bepalend zijn of een boogstraal voor jou bruikbaar is of onhaalbaar
Kortom, een vaste boogstraal is een beperkend gegeven.
Grondplaat (bodemplaat, plattegrond) is hier gebruikt in de betekenis van een programma zoals Wintrack (Grundplatte). Dat is de ontwerpruimte die je ter beschikking staat, het stellende kader, de marges waarbinnen je moet blijven met je baanontwerp.
Er bestaat flexibele rails. Vaak wordt gesteld dat je die alleen kunt gebruiken voor grotere bogen, en dat je voor de standaard bogen ook beter de vaste standaard rails kunt kopen.
Dat is een pragmatisch advies.
D.w.z. standaard rails is makkelijker herbruikbaar, blijft uit zichzelf liggen (er staat geen spanning op de tijdelijk gebogen vorm), en is na gebruik voor meer geld verkoopbaar (met doosje is het waardevast, inflatiebestendig). Dat is allemaal waar, op zich.
Als je voor flexibele rails gaat, dan kun je bepaalde fabrieksstandaards loslaten, zoals vaste boogstralen en vaste hart-op-hart afstanden.
Dat hoeft niet te betekenen dat je het wiel opnieuw gaat uitvinden, want de minimale maten zijn in de jaren '60 van de vorige eeuw vast gelegd in zogenaamde
NEM-normbladen.
Even een plaatje:

Uitleg:
Hier staan 31,3 cm wagons op 4 parallelle boogstralen. Die zijn getekend met een lineaal, gemaakt van verbindingshoekjes (T-stuk van de A*), met dubbelzijdig tape (van de A*) verkleefd aan een aluminium latje. In de lineaal zit een gaatje (middelpunt) waar een spijkertje in past (doorsnede 2 mm).
Zo'n verbindingshoekje past precies tussen de spoorstaven.
Dus viltstiftje boven en onder het t-stuk, en dan heb je de spoorstaven afgetekend.
Op basis van deze tekening zijn (stugge) flexibele rails gebogen is de juiste boogstraal. Stugge flexrails zijn niet geschikt voor bogen. Om ze er toch voor te kunnen gebruiken zijn er met een slijpschijfje in de handboormachine wat stukjes tussen de bielsen weg geschuurd. Teveel weghalen maakt de rails flexibel, te weinig leidt tot een hoekige boogvorm.
Voordeel van deze aanpak: de testrails blijft liggen in de gewenste boogvorm zonder fixeren (zonder lijm). Bijkomend voordeel: de SL-18 puko-strip die op de foto zichtbaar is, kan gemakkelijker tussen de rails worden aangebracht, om er 3-rail van te maken.
De maten van de boogstralen zijn afgeleid van een tabel (afgeleid uit een NEM-normblad):
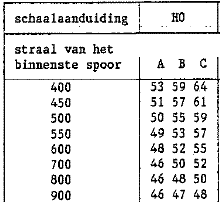
De wagons van 31,3 cm behoren tot type C in deze tabel.
Voor type C begint deze tabel met R=400, en stelt dan dat de volgende boog op 64 mm afstand moet liggen (foutje bij het maken van de lineaal, moet kunnen maar blijkt dus niet te kunnen).
Volgens een ander normblad mogen wagons van type C (max 31,3 cm) pas in een boogstraal van 30x spoorbreedte(30x16,5=495 mm) rijden, d.w.z. dat ze dan aankoppelen bij zacht tegen elkaar aan rijden, dat klopt.
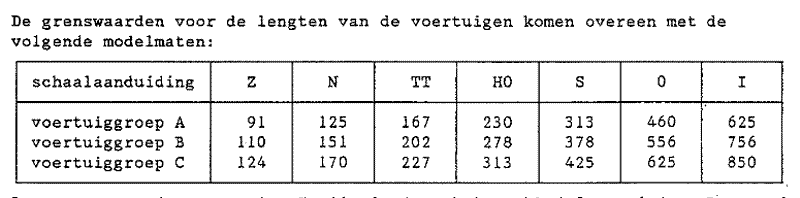 Wat is het maximaal haalbare?
Wat is het maximaal haalbare? Ik ben daarbij uitgegaan van Plaatbreedte (Pb), Bevestigingsbreedte(Bv),
en de Breedte plus Uitzwenking van het voertuig (Be).
Pb=1220 mm
Bv=10 mm (draadstang doorsnede+marge)
Be=een verhaal apart.
Daar komt nog een marge bij, want anders schampt de uitzwenkende trein alsnog een of ander.
AFRONDEN.NAAR.BOVEN (Pb - (2x Bv) - (2x Be) )= 584 mm
Die formule klopt niet helemaal. Normbladen gaan uit van een basisprofiel (B1) van een trein in h0 op rails van 16,5 mm, die basis bij recht spoor is 48 mm, bestaande uit de bakbreedte plus een onbekende marge.
De breedste wagons die ik heb zijn 33 mm. Dat basisprofiel houdt wellicht rekening met bijzondere voertuigen die ik niet heb. Dus heb ik die maat terzijde gelegd.
In bogen komt daar een marge bij voor de uitzwenking naar buiten van de wagon-kop, en de overhang naar binnen van het midden van de wagen-bak. De overhang is aanzienlijk groter dan de uitzwenking, stelt de normtabel. Volgens mij scheelt het hooguit enkele millimeters.
De vraag is, hoe hebben zij dit vast gesteld, is dat dan vergeleken met of zonder de wagonbreedte?
Ik denk zonder, want die maat zit al in hun basisprofiel (B1) verwerkt. En als dat zo is, dan hebben ze geen gebruik gemaakt van lijnmeetkunde, maar van oppervlakteberekeningen.
In de NEM-normtabel staat een gemiddelde waarde van overhang+uitzwenking. Dat is de helft, opdat links en rechts evenveel wordt bijgeteld voor het berekenen van het profiel van de vrije ruimte in bogen.
Het Normblad stelt dat E (dat wat er aan twee kanten bij komt) afhankelijk is van de boogstraal:
bij r=400 =>14 mm, bij r=450 =12 mm, bij r=500 =>11 mm, bij r=550 =>10 mm, enz.
En die waarde moet links en rechts worden bijgeteld bij de breedte van 48 mm.
Maar hoeveel is die overhang, en hoeveel is die uitzwenking, naar verhouding?
Is dat 2 staat tot 1 of 3 staat tot 2, of 10 staat tot 9?
Ergens heb ik dus toch het gevoel het wiel opnieuw uit te moeten vinden (met lijnmeetkunde),
omdat de normbladen uit zijn gegaan van een ander soort wiel (oppervlakte berekeningen).
En dus testte ik het gewoon maar eens uit.
Wat is het minimale?Nu is het minimum, r=400, al een stuk beter dan r=360.
Maar het is niet genoeg voor bepaalde treinen. In 1994 stonden er in de Roco catalogus 3 stoomlocs die vanwege de wielophanging een boogstraal moeten hebben van minimaal 415 mm.
In 2013 meldde een forumgebruiker dat als je een bepaald treinstel in tandem wilt laten rijden, de boogstraal minimaal 420 mm moet zijn (dit vanwege de koppeling).
Vaak is je grondplaat bepalend voor wat je ontwerpt, maar er bestaat ook een wisselwerking tussen wat je wilt en uiteindelijk doet. Op mijn zolder (schuin dak), is b.v. 132 cm diepte (mits op een enkele plek) nog wel te doen, en dat is dan een standaard plaat van 122 cm + een te overbruggen dakmarge.
Veel ontwerpers op dit forum zitten vast aan smallere maten, moeten dus concessies doen aan de boogstralen, en daarmee aan het type voertuigen.
Type B is dan gemakkelijker realiseerbaar dan type C voertuigen omdat de draaicirkel kleiner is.
Als je flexibele boogstralen ontwerpt, dan moet je die beperkingen kennen.
Als je standaard rails koopt, dan kom je er vanzelf wel achter dat sommige modellen
tot een bestaan in de vitrinekast zijn veroordeeld.